

Ressources pour la e année
Tout Leçon Enregistrement affiché Appuis pour les webinaires Appuis pour les leçons
Tout sélectionner Tout effacer
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente de codage du domaine d’algèbre pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Nous ferons un survol des leçons qui ont été créées pour appuyer les enseignantes et les enseignants de l'Ontario ainsi que la pédagogie et les habiletés socioémotionnelles que le codage apporte à votre classe.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
Bienvenue à ce webinaire sur le codage en lien avec notre nouveau programme-cadre de Mathématiques 2020. Nous vous ferons découvrir la pédagogie et les habiletés socioémotionnelles que le codage apporte dans votre classe, ainsi que les leçons qui ont été créées pour aider les enseignants de l'Ontario au cycle moyen.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
Bienvenue à ce webinaire sur le codage en lien avec notre nouveau programme-cadre de Mathématiques 2020. Nous vous ferons découvrir la pédagogie et les habiletés socioémotionnelles que le codage apporte dans votre classe, ainsi que les leçons qui ont été créées pour aider les enseignant.e.s de l'Ontario au cycle primaire.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
 Principaux changements - Programme-cadre de mathématiques de l'Ontario, de la 1re à la 8e année, 2020
[PDF]
Principaux changements - Programme-cadre de mathématiques de l'Ontario, de la 1re à la 8e année, 2020
[PDF]
Ce document, élaboré par le Ministère de l'Éducation de l'Ontario, compare sous forme de tableau les principaux changements entre le programme-cadre de mathématiques 1re-8e de 2005 et celui de 2020.
 Domaine A : Apprentissage socioémotionnel et processus mathématiques (aperçu du domaine)
[PDF]
Domaine A : Apprentissage socioémotionnel et processus mathématiques (aperçu du domaine)
[PDF]
Continuum pour le domaine d'étude A : Apprentissage socioémotionnel et processus mathématiques. Ce PDF d'une page permet de voir les liens entre les habiletés socioémotionnelles et les processus mathématiques. À noter que ce domaine n'a pas de contenu d'apprentissage.
 Domaine B : Nombres (aperçu 1re-8e)
[PDF]
Domaine B : Nombres (aperçu 1re-8e)
[PDF]
Continuum pour le domaine d'étude B : Nombres. Ce PDF montre les attentes ainsi que la progression des contenus d'apprentissage de la 1re à la 8e année.
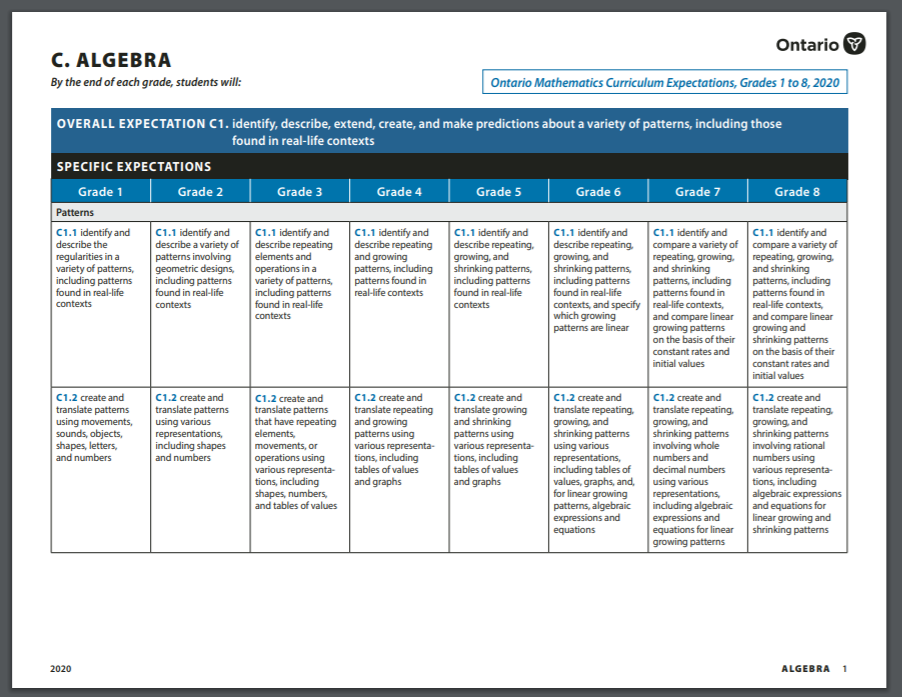 Domaine C: Algèbre (aperçu du domaine)
[PDF]
Domaine C: Algèbre (aperçu du domaine)
[PDF]
Continuum pour le domaine d'étude C : Algèbre. Ce PDF montre les attentes ainsi que la progression des contenus d'apprentissage de la 1re à la 8e année.
 Domaine D :Données (aperçu du domaine)
[PDF]
Domaine D :Données (aperçu du domaine)
[PDF]
Continuum pour le domaine d'étude D : Données. Ce PDF montre les attentes ainsi que la progression des contenus d'apprentissage de la 1re à la 8e année.
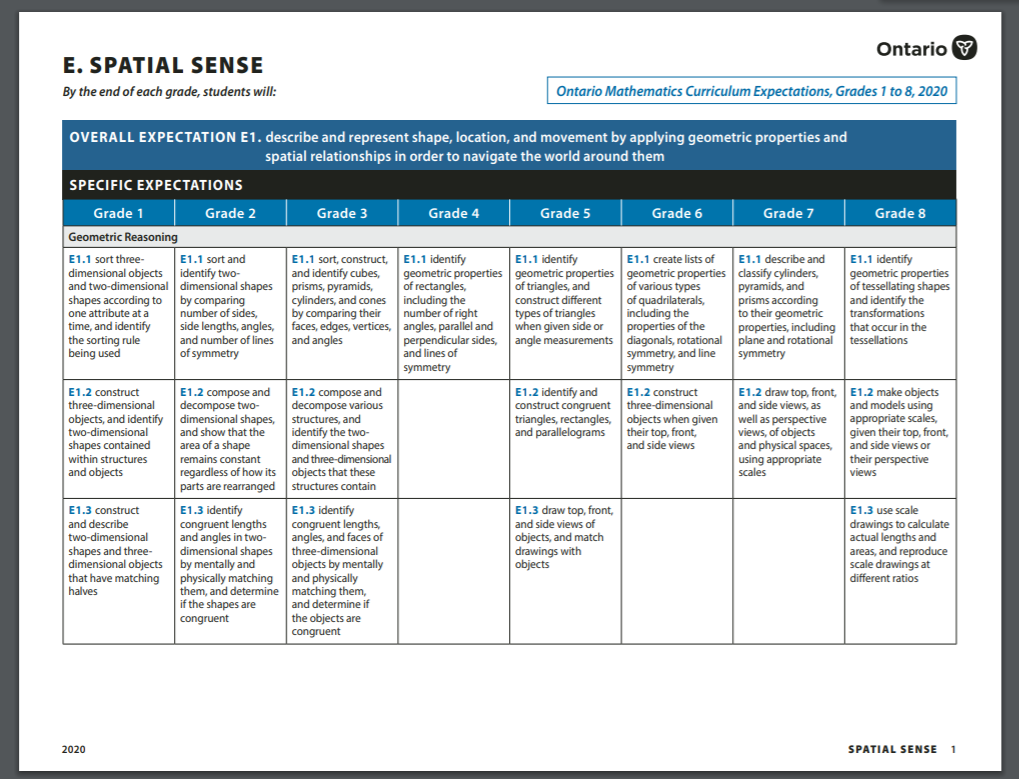 Domaine E : Sens de l'espace (aperçu du domaine)
[PDF]
Domaine E : Sens de l'espace (aperçu du domaine)
[PDF]
Continuum pour le domaine d'étude E : Sens de l'espace. Ce PDF montre les attentes ainsi que la progression des contenus d'apprentissage de la 1re à la 8e année.
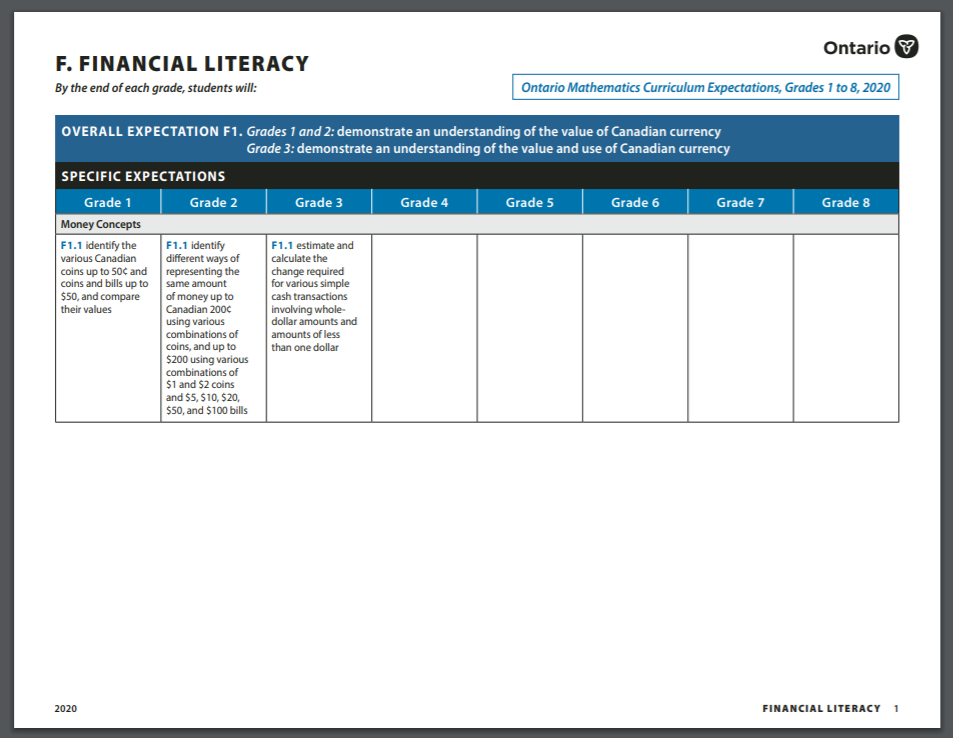 Domaine F : Littératie financière (aperçu du domaine)
[PDF]
Domaine F : Littératie financière (aperçu du domaine)
[PDF]
Continuum pour le domaine d'étude F : Littératie financière. Ce PDF montre les attentes ainsi que la progression des contenus d'apprentissage de la 1re à la 8e année.
 Programme-cadre de mathématiques de l'Ontario, 2020, 1re à la 8e année
[URL]
Programme-cadre de mathématiques de l'Ontario, 2020, 1re à la 8e année
[URL]
Ce programme-cadre est destiné aux écoles de langue française; il remplace «Le curriculum de l’Ontario de la 1re à la 8e année – Mathématiques (2005)». À partir de septembre 2020, tous les programmes de mathématiques de la 1re à la 8e année seront fondés sur les attentes et les contenus d’apprentissage présentés dans ce programme-cadre.
 Programme-cadre de mathématiques de l'Ontario, 2021, 9e année
[URL]
Programme-cadre de mathématiques de l'Ontario, 2021, 9e année
[URL]
Ce programme-cadre est destiné aux écoles de langue française; il remplace «Le curriculum de l’Ontario de la 1re à la 8e année – Mathématiques (2005)». À partir de septembre 2021, tous les programmes de mathématiques de la 9e année seront fondés sur les attentes et les contenus d’apprentissage présentés dans ce programme-cadre.
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. Les scénarios donnent l'occasion d'avoir une discussion sur les choix financiers et les inégalités d'accès &
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle moyen du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. Les scénarios donnent l'occasion d'avoir une discussion sur les choix financiers et les inégalités d'accès à ces cho
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle primaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. L'objectif des leçons était de fournir des contextes réels pour que les élèves développent leur compréhension
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle intermédiaire du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle moyen du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle primaire du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Il s'agit d'une série de 5 leçons, basées sur des contes de fées bien connus, qui invitent les élèves à apprendre le pseudocodage par des mouvements simples liés au raisonnement spatial.
Dans cette leçon, les élèves se pratiquent à se donner des directives les uns les autres pour se déplacer autour de différents obstacles sur une grille géante vers un point d'arrivée.
Dans cette leçon, les élèves sont mis au défi de trouver un trajet pour un joueur de hockey en contournant de nombreux obstacles sur la patinoire jusqu'au filet de l'équipe adversaire.
Il s'agit d'une série de 3 leçons, centrées sur des animaux de la ferme, qui invitent les élèves à cheminer dans leurs apprentissages en passant de l'utilisation du vocabulaire lié à la position, du déplacement et du mouvement physique à l'apprentissage du pseudo code avec des chiffres et des flèches.
Les élèves apprennent à animer un personnage (sprite) en utilisant Scratch ou une plateforme de codage en bloc similaire afin que le personnage se déplace de gauche à droite sur un écran d'ordinateur.
Dans cette leçon, les élèves analysent les attributs des pièces de monnaie, jouent à des jeux utilisant les attributs, créent leurs propres pièces de monnaie et comparent les attributs des pièces canadiennes avec les pièces imaginées. Ce faisant, ils apprennent à reconnaître et à décrire les pièces par leurs attributs, par exemple la taille, la forme, la couleur, l'image et la texture, ainsi que la valeur des pièces canadiennes en fonction de leurs attributs.
J’adore mon nom ! Les élèves utiliseront des pièces de monnaie pour « acheter » les lettres de leur nom afin de fabriquer une plaque d'identité. Ce faisant, les élèves apprennent à comparer la valeur des pièces de monnaie canadiennes.
Dans cette leçon, les élèves apprennent à faire un modèle mathématique afin de prédire le nombre de bonbons nécessaires pour un sac de bonbons. Il s'agit principalement de déterminer les questions importantes auxquelles il faut répondre, les informations manquantes nécessaires pour résoudre le problème et émettre des suppositions sur les informations manquantes.
Dans cette leçon, les élèves de première année développent un modèle mathématique pour essayer de prédire quels nouveaux meubles de maison de poupée plairaient le plus aux élèves du Jardin d'enfants avant qu'ils ne soient achetés.
Dans cette leçon, les élèves apprennent à diviser les différentes formes et objets en parties égales à partager, à utiliser le vocabulaire mathématique comme les demis et les quarts pour décrire des parties égales et à comprendre que plus il y a de parties égales, plus les portions sont petites.
La classe fait une visite imaginaire au zoo. Pendant la visite, la classe va nourrir certains des animaux. La classe a un budget limité et ne peut donc acheter qu'une quantité limitée de collations. Ils ne peuvent nourrir que 2 girafes, 4 lions, 2 chimpanzés, 4 zèbres et 2 éléphants. Les élèves travaillent en dyades ou en petits groupes pour décider de la façon de répartir équitablement la nourriture entre chaque type d'animal, en veillant à respecter les préférences des animaux.
Les élèves utilisent leur imagination pour faire semblant qu'ils vont au zoo pour une journée afin de travailler avec les gardiens du zoo en tant qu'assistants. L'une de leurs tâches consiste à répartir une certaine quantité de nourriture de façon équitable entre les deux ours polaires. Ils doivent également répartir les mêmes quantités entre 4 grizzlis et 10 ours noirs.
Dans cette leçon, les élèves imaginent qu'un zoo accueille de nouveaux animaux et qu'ils sont chargés de concevoir et de construire de nouveaux enclos pour eux. Le défi est que l'espace est limité. Les élèves utilisent leurs connaissances des fractions pour concevoir les nouveaux enclos.
Dans cette leçon, les élèves devront écrire des codes débranchés en utilisant une séquence d'actions sur un tapis de 100 ou une grille 10 x 10 pour ramasser suffisamment de pièces équivalant à 75 ¢ pour acheter un marqueur.
Dans cette leçon, les élèves vont créer et exécuter une séquence de danses contenant des instructions débranchées et précises pour effectuer les danses.
Dans cette leçon, les élèves apprennent à utiliser des dispositifs de codage pour faire du codage séquentiel branché pour créer des phrases mathématiques à l'aide d'une grille de 100 nombres.
Dans cette leçon, les élèves liront une histoire et aideront l'écureuil à trouver, partager et cacher des glands dans la forêt et à résoudre des problèmes en utilisant des habiletés de codage.
Dans cette leçon, les élèves vont calculer des sommes allant jusqu'à 100 $ pour de l'équipement de récréation.
Dans cette leçon, les élèves trouveront plusieurs façons de représenter 200 $ afin de décider quelle monnaie ils aimeraient recevoir de la ville pour leurs matériaux de recyclage.
Dans cette leçon, les élèves travailleront sur les 2 premières composantes du processus de modélisation mathématique. Ils détermineront comment organiser l'espace de matériel de manipulation mathématiques pour une classe de 2e année.
Dans cette leçon, les élèves apprennent à comprendre les 2 premières composantse de la modélisation mathématique. Ils élaborent un plan spatial pour un événement de deuxième année dans la cour d'école.
Créer une grille de critères pour évaluer comment une séquence de mouvements pour l'APQ peut inspirer les élèves à bouger - dans cette leçon, les élèves apprennent à comprendre et à développer les 4 étapes du processus de modélisation mathématique. Le concept de temps est discuté en tant que critère possible pour évaluer.
Split, l'écureuil, partage ses graines - dans cette leçon, les élèves apprennent à créer des situations de partages équitables de un tiers et deux sixièmes entre 3 écureuils.
Dans cette leçon, la grand-mère de Wooly tricote différentes combinaisons de couleurs comme rayures sur des chandails pour représenter un demi, deux quarts, un tiers et deux sixièmes (modèle de surface). Elle tricote ensuite ses foulards avec des pompons ayant les mêmes fractions que les chandails (modèle d'ensemble). Les fractions équivalentes sont ensuite comparées pour chaque modèle. Les élèves représentent toutes ces fractions avec différents matériels de manipulation dans 2 centres d'apprentissage. Les photos des représentations peuvent ensuite être utilisées pour des jeux de cartes.
Dans cette leçon, les élèves représentent la multiplication sous forme d'addition répétée de groupes égaux, y compris des groupes d'un demi et d'un quart, et déterminent la quantité d'argile nécessaire à acheter pour que la classe crée de l'art. Ils utilisent divers outils et schémas pour résoudre le problème.
Dans cette leçon, les élèves représentent et résolvent des problèmes de partage équitable d’un tout pouvant comprendre jusqu’à 10 poissons séchés entre un certain nombre de personnes. Les résultats sont des nombres fractionnaires. Des liens à des activités autochtones sont proposées comme contexte.
Les élèves s'engagent dans une leçon débranchée qui explore le sens de l'espace (position et déplacement) ainsi que le codage. Il y a également des liens avec la communication orale. Les élèves donneront à leur partenaire un ensemble de consignes qui leur permettront de se déplacer dans la classe en utilisant des stratégies de codage.
Dans cette leçon, les élèves exploreront la répétition de motifs par la danse en utilisant un outil de codage en ligne et leur propre corps. Cette leçon explore les habiletés de codage et fait des liens avec la danse.
Dans cette leçon, les élèves auront l'occasion d'estimer la monnaie à rendre en utilisant des pièces de monnaie et en déboguant le code. Ils exploreront la littératie financière et le codage.
Dans cette leçon, les élèves créent des tables de valeurs représentant des suites à motif croissant et décroissant pour résoudre des problèmes en remixant le code. On y aborde plusieurs attentes du domaine de l'algèbre.
Dans cette leçon, les élèves travaillent sur le concept d’arrondir au plus près de 5 et 10 et de rendre la monnaie dont la somme est inférieure à un dollar. Elle explore également la façon dont les pièces de un cent sont utilisées dans les transactions en argent comptant et virtuellement. Elle offre l'occasion de discuter du rôle de la pièce de monnaie dans la vie courante. La leçon « Qu’est-il arrivé à la pièce de un cent ? » est la première de deux leçons. La leçon complémentaire, « Rendre la monnaie », est la deuxième leçon de ce duo. La leçon Rendre la monnaie se retrouve dans les le&cce
Cette leçon examine ce que signifie le mot valeur et comment cela se rapporte à l'argent. Les élèves explorent comment de la monnaie peut avoir de la valeur. Dans cette leçon, les élèves estiment et trouvent la valeur d’un ensemble de pièces de monnaie. Ils estiment et calculent la monnaie à rendre pour des transactions en argent comptant comportant des montants de moins de un dollar.
Dans cette leçon, les élèves s’engagent dans trois des composantes du processus de modélisation mathématique (comprendre le problème - questions, analyser la situation - collecte d’informations et formuler des suppositions et créer un modèle). En utilisant une situation réelle sur l’usage des appareils électroniques de classe, les élèves travaillent ensemble pour émettre un modèle simple et procéder à une collecte des données. Cette leçon sera suivie d’une deuxième leçon intitulée: « On recharge nos batteries ! » où les élèves poursuivent leur apprentissage du processus de modélisat
Dans cette leçon, les élèves continuent de développer, d’analyser et de parfaire le modèle mathématique présenté à la leçon 1: « Panne de courant ! » Ils ont la possibilité de collecter et d'interpréter des données supplémentaires pour répondre à d’autres questions, de créer de nouveaux modèles et de rechercher des solutions pratiques à la situation donnée.
Dans cette leçon, les élèves ont l'occasion d'appliquer le processus de modélisation mathématique à une situation de la vraie vie qui est directement liée au programme-cadre de sciences. Sur une période de plusieurs mois, ils feront l'expérience répétitive de la modélisation mathématique en posant des questions, en s'engageant dans des explorations et des enquêtes scientifiques, en faisant une collecte des données, en développant et en analysant leurs modèles qui seront utilisés dans une situation authentique. Le résultat ultime de cette leçon - une vente de plantes - qui donnera également la possibilité d'applique
Dans cette leçon, les élèves développent des modèles mathématiques qui tiennent compte de la taille des pots de plantes et de l'espace disponible en utilisant à la fois des habiletés et des concepts de mesure et de nombres. Les élèves participent à toutes les étapes du processus de modélisation mathématique afin de résoudre un problème et de déterminer comment les pots peuvent être placés de manière organisée à mesure qu'ils grandissent. Au cours du processus, ils établissent des liens avec le programme-cadre de sciences et si vous le souhaitez, la leçon peut être liée à la leçon 3 de mod&
Dans cette leçon, les élèves explorent le monde des fractions et des fractions équivalentes à travers une course de vélo en utilisant une résolution de problème en trois temps. Elle offre la possibilité de représenter des fractions à l'aide d'un modèle de longueur. Quelques jeux sont également inclus afin d'aider les élèves à consolider le concept de fraction en utilisant les différentes représentations.
Cette leçon permet aux élèves de travailler avec des fractions équivalentes tout en solutionnant des problèmes de partage équitable. Les élèves sont encouragés à explorer différentes unités fractionnaires tout en renforçant l'importance du partage équitable et d’utiliser plusieurs façons de nommer ou de représenter des fractions.
Dans cette leçon, les élèves auront l’occasion de créer une carte de remerciement tout en appliquant des concepts de fractions. Ils devront dans un premier temps, diviser leur carte en utilisant des demis, des tiers et des quarts. Ensuite, ils détermineront le nombre d’autocollants à utiliser pour décorer leur carte.
Utilisez des directives codées pour effectuer des translations sur une grille.
Utilisation de mouvements physiques avec le codage afin de créer des motifs répétitifs pour décrire les translations (séquentielles et répétitives).
Introduction au codage sur un plan cartésien en utilisant des paires de coordonnées dans le premier quadrant; papier quadrillé (codage débranché) et Scratch.
Les élèves vont créer une formule de codage dans Scratch pour trouver l'aire d'un rectangle afin de pouvoir peindre les murs de la classe. Cette leçon aborde également des attentes des domaines du sens de l'espace et de la littératie financière.
Utiliser le vocabulaire mathématique pour faire des prédictions d'une probabilité (pile ou face) et utiliser un code (Scratch) pour représenter cette situation.
Utiliser différentes stratégies d'estimation afin de déterminer le meilleur prix de plusieurs articles en trouvant le taux unitaire.
Dans cette leçon, les élèves vont réfléchir aux facteurs qui influencent leurs décisions lors d'un achat. Les enseignant(e)s peuvent explorer deux scénarios (un achat pour un désir et un achat pour un besoin). Les élèves pourront prendre une décision et justifier leur choix en utilisant les facteurs pouvant influencer les comportements en matière de dépense et d’épargne.
Cette leçon est la première d'une série de deux. Les élèves entament les trois premières étapes du processus de modélisation mathématique soient comprendre la situation, analyser la situation et créer un modèle mathématique. À partir d'une activité authentique, les élèves travaillent ensemble pour émettre un modèle simple et procéder à une collecte des données. Cette leçon sera suivie d’une deuxième leçon intitulée: « On sert le petit-déjeuner ! » où les élèves poursuivent leurs apprentissages du processus de modélisation mathématique.
Dans cette leçon, les élèves continuent d’analyser, d'évaluer leur modèle mathématique présenté à la première leçon (Préparer le petit-déjeuner de l'école) pour ensuite, le modifier au besoin. Ils ont la possibilité de collecter et d'interpréter des données supplémentaires pour répondre à d’autres questions, de créer de nouveaux modèles et de rechercher des solutions pratiques à la situation donnée.
Les élèves utiliseront un modèle mathématique pour les aider à déterminer les meilleurs achats à effectuer dans un scénario fictif de jeu vidéo.
Créer des schémas pour comprendre le sens du numérateur et du dénominateur des fractions écrites en notation fractionnaire usuelle.
Dans cette leçon, les élèves auront la chance de comparer des fractions dans deux différents scénarios de partage équitable d'une quantité. Ils pourront les comparer avec différentes représentations de la fraction.
Dans cette leçon, l'élève compte les fractions unitaires afin de l'aider à représenter la relation entre l'addition répétée de fractions unitaires et la multiplication de ces mêmes fractions unitaires par un nombre naturel.
Budget et feuille de calcul : une planification financière - Dans cette leçon, les élèves comprendront comment la feuille de calcul peut aider à gérer un budget, à ajuster ou modifier les codes pour faire des changements dans une feuille de calculs d’un budget et à cerner la différence entre des besoins et des désirs pour équilibrer un budget.
La navigation par codage - débranché - Dans cette leçon, les élèves vont créer un code pour suivre un trajet de voyage en utilisant des coordonnées, des formes, les descriptions de position et déplacement. Ils auront même à faire face à certains détours.
Se rappeler des faits de multiplication avec le codage - Dans cette leçon, les élèves apprendront comment se rappeler et démontrer les faits de multiplication et division jusqu'à 12 x 12 en utilisant et en manipulant un code existant. Ils appliqueront ce code à une feuille de calculs pour créer des illustrations originales.
Dans cette leçon, les élèves pourront établir des équivalences entres des nombres décimaux et des fractions par l'exploration de suites en utilisant le codage avec Scratch. Ils pourront utiliser des données pour faire des prédictions et prolonger les suites.
Dans cette leçon, les élèves vont réfléchir à l'importance d'un budget. Les enseignant(e)s peuvent explorer un de deux scénarios (amasser de l'argent pour une sortie ou gagner de l'argent grâce à un emploi de gardien ou gardienne). Les élèves prendront en considération pourquoi ils voudraient gagner de l'argent, comment gagner une somme et mettre en priorité ses dépenses.
Dans cette leçon, les élèves apprendront à estimer et à calculer les coûts totaux (y compris la TVH) et à les comparer au montant d’argent qu’ils ont. Ils feront une visite de restaurants pour estimer et ensuite calculer les coûts en sélectionnant des items sur le menu.
Dans cette leçon, les élèves apprennent à comparer les prix de différents articles. Plusieurs articles sont vendus dans des paquets de différentes tailles. Quel est le meilleur prix ? Y a-t-il d’autres facteurs qui peuvent influencer les achats que vous faites ? Les élèves apprennent diverses stratégies, y compris la recherche de taux unitaires, pour prendre des décisions financières.
Dans cette leçon, les élèves créent une échelle d'évaluation pour les aider à analyser et à choisir les activités d'APQ pour leur classe. Ils s’engagent dans le processus de modélisation mathématique en travaillant en collaboration pour émettre des suppositions, créer un modèle (leur système d'évaluation) le tester et réviser ce modèle.
Dans cette leçon, les élèves vont aborder le temps d’écran. Plusieurs experts pensent que les enfants devraient limiter le temps d’écran. Les parents veulent soutenir leurs enfants pour leur montrer à faire de bons choix quant au nombre de minutes sur les écrans et quelles activités pourraient être plus ou moins bénéfiques. Les élèves s’engagent dans le processus de modélisation mathématique pour développer un outil que les parents et les enfants pourraient utiliser pour surveiller leur temps d’écran et faire de bons choix quant aux activités passées sur les écrans.
Dans cette leçon, les élèves analyseront comment les produits frais sont fournis de façon fiable aux personnes qui vivent dans des communautés éloignées en Arctique. Ils réfléchiront aux coûts de transport, la capacité de construire des serres et de vivre dans des communautés éloignées.
Dans cette leçon, les élèves pourront explorer la relation entre les fractions, les nombres décimaux et les pourcentages. Les élèves travaillent dans une présentation interactive Google Slides en ligne pour explorer et apprendre tout en utilisant les visuels et le matériel de manipulation virtuel.
Dans cette leçon, les élèves apprendront à multiplier un nombre naturel par une fraction unitaire en utilisant une variété de stratégies. Ils partageront également des stratégies qu’ils préfèrent. Les élèves utiliseront du matériel concret et d’autres outils visuels pour les aider à comprendre les différentes stratégies.
Dans cette leçon, les élèves explorent diverses représentations de fractions (modèle de surface, modèle d’ensemble et modèle linéaire). Ensuite, ils sont mis au défi d’utiliser ces modèles pour représenter et résoudre plusieurs problèmes qui les obligent à comparer les fractions, y compris les nombres fractionnaires et les fractions impropres.
Dans un environnement débranché, les élèves coderont des transformations--combinaisons de translations et de réflexions--sur le plan cartésien en écrivant et en exécutant un pseudocode. Cette leçon peut être utilisée avant la leçon «Codage des transformations - débranché ! »
Dans un environnement débranché, les élèves coderont des transformations--combinaisons de translations et de réflexions--sur le plan cartésien en écrivant et en exécutant un pseudocode.
En créant un pseudo-code pour les actions afin de déterminer quel nombre entier est plus grand qu'un autre, les élèves identifient les blocs de codage Scratch qui effectueront ces actions. Ils peuvent remixer un exemple de projet Scratch ou programmer le leur à partir d'un projet Scratch de départ. L'utilisation d'une droite numérique dans les projets de codage donne une représentation visuelle des entiers. Remarque: pour les enseignants qui ne sont pas familiers avec le codage Scratch, des instructions sont incluses pour vous aider à enseigner ces leçons.
Création d'un pseudo-code pour les actions afin de déterminer les actions utilisées lors de l'utilisation d'une « machine à fonctions:entrée / sortie », les élèves identifient ensuite les blocs de codage Scratch qui réaliseront ces actions. Ils peuvent remixer un exemple de projet Scratch ou programmer le leur à partir d'un projet Scratch de départ. Cette leçon et celle de : « Quelle est la plus grande ? » misent sur la compréhension de vos élèves des nombres entiers positifs et négatifs. Remarque: pour les enseignants qui ne sont pas familiers avec le codage Scratch, des instructions sont incluses pour vous aider à enseigner ces le&cce
Dans cette leçon, les élèves coderont à l'aide de Google Sheets ou de tout autre tableur. Les élèves créeront un budget pour aider à planifier un objectif financier tout en tenant compte des revenus et des dépenses.
Grâce à l'utilisation du pseudo-code, les élèves apprendront à décomposer leur pensée mathématique concernant les concepts de nombres premiers et composés et d'algorithmes; identifier les facteurs des nombres composés comme une série d'actions; connecter ces actions pour bloquer le codage et, ce faisant, renforcer leur pensée computationnelle. Remarque: Pensez à utiliser cette leçon de codage après que les élèves comprennent comment représenter des nombres composés à l'aide de l'arbre de facteurs. Pour les enseignants qui ne sont pas familiers avec le codage Scratch, des instructions sont incluses pour vous aider à enseig
Dans cette leçon, les élèves apprendront à comparer différentes méthodes de paiement - en identifiant les avantages et les désavantages - et les meilleures façons de les utiliser. Les élèves analyseront et identifieront également comment divers taux d'intérêt sont appliqués aux différents modes de paiement afin de faire la meilleure décision financière possible quand ils font des achats.
Dans cette leçon, les élèves réfléchiront à la façon dont les ressources sont distribuées par le biais de dons, d'échanges, de prêts et d'emprunts grâce à la création d'un projet communautaire.
Dans cette leçon, les élèves identifieront les types d'objectifs financiers et comment les atteindre, ainsi que les facteurs qui les aident ou les empêchent de les atteindre. Les élèves continueront ensuite à travailler vers l'atteinte des résultats d'apprentissage de la leçon dans un contexte de projets -en préparant et en présentant un argument convaincant sur la manière dont ils pourront atteindre leur but.
Dans cette leçon, les élèves se retrouvent face à un problème compliqué du monde réel. Une petite bibliothèque gratuite a été donnée à l'école. « Quels livres faut-il pour continuer à assurer le succès de la petite bibliothèque ? » Les élèves feront leurs propres suppositions et décisions au fur et à mesure qu'ils développent un système d'évaluation pour prédire la probabilité qu'un livre soit lu. Des suggestions pour prolonger l'activité au-delà du processus de la modélisation mathématique à ce qui est nécessaire pour gérer une vrai
Dans cette leçon en deux parties, les élèves s'engageront dans le processus de modélisation mathématique pour créer un modèle qui aide les consommateurs à comprendre leurs habitudes de consommation d'électricité et / ou quel modèle de tarification répond mieux à leurs besoins.
Dans cette leçon, les élèves considèrent l'idée de faire un jardin scolaire. Nous vivons dans une province vaste et variée. Les élèves élaborent un modèle pour prédire les probabilités de succès de divers plans de jardins. Ce modèle sera utilisé par d'autres, par exemple un groupe de parents, pour décider du jardin gagnant conçu par les élèves. Parmi les autres activités, on trouve des informations sur la création d'un jardin et l'étude des objectifs de développement durable en sciences sociales.
Les élèves utiliseront des modèles visuels et concrets, y compris des droites numériques, pour approfondir leur raisonnement sur la façon dont les fractions peuvent être combinées par addition.
Dans cette leçon, les élèves utiliseront du matériel de manipulation, des applications virtuelles et des simulations pour explorer les relations entre les fractions. L'apprentissage est axé sur des situations concernant le processus de fabrication des lacets de chaussures. La consolidation supplémentaire comprend des idées d'art visuel pour les motifs et les dallages.
Dans cette leçon, les élèves apprendront à multiplier et à diviser des nombres naturels par des fractions propres en calculant la quantité de tissu utilisée lors de la création des bannières de classe.
Dans cette leçon débranchée, les élèves utilisent la pensée computationnelle afin de déplacer un objet (le loup) dans le plan cartésien, en utilisant des translations et des rotations. Le but ultime est de déplacer le loup afin qu'il puisse rejoindre ses louveteaux. Deux variations sont proposées ici: la première voit le loup se déplacer librement dans le plan sans obstacle et la deuxième nécessite l'addition de de blocs (codes) afin d'éviter des rivières et fossés.
Durant cette leçon, les élèves ont la chance de créer le prototype d'une application pour commander au restaurant. En utilisant des blocs de conditions et d'opérations de Scratch, les élèves exploreront des attentes du domaine de Nombres en calculant le coût total d'un repas. Divers scénarios (avec différents items ou différentes quantités) sont proposés afin de différencier la leçon.
En utilisant le programme Scratch, les élèves ont l'occasion de créer une calculatrice avec laquelle ils peuvent comparer deux différents types de rabais. Dépendant du nombre d'articles achetés, la calculatrice sera en mesure de fournir des économies en choisissant soit une remise de 20 %, soit une remise de 20 $. Les élèves utilisent les blocs de conditions et d'opérations dans cette activité.
À travers l'histoire et la beauté des mathématiques, les élèves découvrent l'importance des mathématiques dans la vie de tous les jours, incluant les jeux vidéos ! Ils peuvent ensuite utiliser Scratch afin de coder une séquence d'instructions (code) afin de déplacer un avatar dans un labyrinthe. Les élèves explorent les concepts de rotation, de translation, des angles et des distances, tout en jouant. On leur demande également de penser à une séquence d'instructions afin de déplacer un avatar d'un point à l'autre.
Dans cette leçon, les élèves sont conscientisés sur l'importance d'établir un budget; de connaître les différents types de comptes d'épargnes et comment les taux d'intérêts peuvent affecter leurs économies. Les élèves vont aussi évaluer l'utilisation des revenus gagnés d'un emploi à temps partiel dans le choix des téléphones cellulaires. Pour terminer, ils vont aussi évaluer les avantages et les coûts des forfaits cellulaires.
Les élèves utilisent de l'argent fictifs afin d'apprendre comment convertir entre deux devises, canadien et américain. Ils vont apprendre la raison d'être et la logique en arrièrer de la conversion des devises étrangères et comment utiliser les sites web de taux quotidiens afin de trouver le montant obtenu de l'autre devise.
Dans cette leçon, les élèves analyseront différents scénarios afin d'identifier les facteurs qui influencent la prise de décision financière. Les élèves évalueront l'impact de chaque facteur sur le processus de prise de décision et la manière dont ils influencent les objectifs financiers à court et à long terme.
Dans cette leçon, les élèves vont créer un modèle mathématique, vont faire une collecte de données et vont les organiser afin de déterminer l'impact d'une politique de lavage des mains d'un conseil scolaire. Les élèves utiliseront leur modèle pour faire des prédictions, puis ils testeront ces prédictions en jouant le scénario du lavage des mains. À la fin, les élèves présenteront leur conseils sur la politique, en utilisant des arguments mathématiques basés sur les informations fournies par leurs modèles.
Forêts en crise - Dans cette leçon, les élèves appliqueront le processus de modélisation mathématique pour analyser les données sur les taux actuels de déforestation au Canada. Les élèves créeront un modèle qui pourra être utilisé pour prédire le point auquel nous n'aurons plus assez de produits forestiers pour répondre à nos besoins.
Dans cette leçon, les élèves vont créer un modèle, faire une collecte de données et les organiser afin de prédire les 10 meilleurs athlètes professionnels dans un sport donné. Les élèves utiliseront leur modèle pour faire et tester des prédictions par rapport aux joueurs de hockey qui devraient être choisis pour une ligue de hockey simulé.
Dans cette leçon, les élèves travaillent avec une recette de pizza fictive pour multiplier et diviser des nombres naturels par des fractions et multiplier et diviser des fractions par d'autres fractions. Les élèves utiliseront ensuite leur compréhension de la multiplication et de la division de fractions par d'autres fractions afin de créer et de résoudre leurs propres problèmes.
Dans cette leçon, les élèves collaborent pour représenter visuellement et résoudre une variété de problèmes comportant des fractions. Les élèves comprendront mieux quand et pourquoi ils devraient utiliser l'addition, la soustraction, la multiplication ou la division lorsqu'ils travaillent avec des fractions.
Les élèves utilisent des fractions et les minutes d'une heure afin de créer un horaire de visite au zoo. Plusieurs scénarios vont leur permettre de travailler les opérations avec les fractions, les fractions équivalentes et aussi des nombres fractionnaires.
Dans cette leçon, les élèves travaillent les transformations successives dans un plan cartésien. Les élèves combineront leurs habiletés en géométrie et en codage pour déchiffrer des codes existants, en effectuant du débogage des codes et trouvant des erreurs.
Grâce à la magie du codage, les élèves explorent les propriétés des formes géométriques ainsi que les différentes transformations géométriques.
Dans cette leçon, les élèves augmenteront leur compréhension du théorème de Pythagore tout en travaillant leurs habiletés en codage.
Vos élèves veulent-ils devenir des Youtubeurs célèbres ? Les élèves apprendront à rentabiliser une chaîne YouTube et à utiliser le codage pour prédire les revenus qu'une vidéo YouTube peut générer.
Dans cette leçon, les élèves analysent différentes façons dont les intérêts sont calculés, facturés et gagnés. Les élèves comparent des scénarios pour comprendre l'impact de l'intérêt.
Cette leçon se voit être une leçon d'introduction aux cartes de crédit. Les élèves en apprendront sur les avantages et les désavantages de l'utilisation des cartes de crédit en comparant les taux d'intérêt, les frais annuels, les systèmes de récompenses et autres.
Dans cette leçon, l'élève apprend à faire et à maintenir un budget équilibré en utilisant divers outils de budget.
Dans cette leçon, les élèves utilisent leurs connaissances de littératie financière et leurs habiletés en recherche afin de trouver le meilleur endroit pour leur voyage de fin d'année. Ils devront prendre en considération les coûts, la supervision, la distance. Ainsi, ils pourront découvrir ce que leur communauté et les alentours peuvent leur offrir.
Dans cette leçon, les élèves tenteront de découvrir ce qui est nécessaire pour devenir une grande vedette sur Youtube. Ils devront trouver les éléments qui font en sorte qu'un individu est propulsé au sommet des classements Youtube. En utilisant ces informations, les élèves devront créer un modèle qui sera en mesure de prédire les vedettes de Youtube pour les années à venir.
Dans cette leçon, les mathématiques et les sciences s'unissent pour former une occasion d'apprentissage ouverte et engageante. Les élèves examinent la richesse en eau du Canada afin de déterminer à quel moment les rôles seront inversés. En regardant les divers facteurs qui contribuent à la richesse, à l'approvisionnement et à l'utilisation de l'eau au Canada, ils réfléchissent aux suppositions qu'ils émettent pour créer un modèle mathématique.
Est-ce que les fractions sont utilisées adéquatement dans les publicités ? En analysant des affiches publicitaires, les élèves pourront répondre à cette question.
Dans cette leçon, les élèves découvrent et apprennent à diviser des fractions par des nombres naturels, diviser des nombres naturels par une fraction et diviser des fractions par des fractions à l'aide de schémas et de matériel de manipulation.
Dans cette leçon, les élèves s'exerceront à additionner, soustraire, multiplier et diviser des fractions en jouant à des jeux.
Modèle d’un plan de cours (option 1) créé par l'équipe OAME/AFEMO. Mathématiques 9e 2021. Organisé par les applications des concept. Ce plan de cours organise les attentes et les contenus du cours MTH1W en 10 questions.
Modèle d’un plan de cours (option 2) créé par l'équipe OAME/AFEMO. Mathématiques 9e 2021. Organisé par questions et par sujets. Ce plan de cours organise les attentes et les contenus du cours MTH1W en cinq unités.
Modèle d’un plan de cours (option 3) créé par l'équipe OAME/AFEMO. Mathématiques 9e 2021. Organisé par regroupement des concepts. Ce plan de cours est organisé en regroupant les attentes selon quatre idées unifiées.
Les élèves de l'Ontario vivent dans un monde complexe qui est régi par les données. Ce monde évolue et l'émergence de nouveaux domaines et de nouvelles carrières nécessite des personnes ayant un niveau élevé de littératie des données. Soutenir les élèves dans l'acquisition de compétences critiques en littératie des données est une composante essentielle du nouveau curriculum de 9e année décloisonné. La littératie des données est différente de la gestion des données. Bien sûr, les compétences en gestion des données sont aussi importantes pour analyser les données. Dans le cadre du programme-cadre de mathématiques élémentaire révisé en 2020, les élèves ont développé leurs compétences en gestion des données. Comment les relier à l'objectif plus large de la littératie des données ? Quelles sont les compétences nécessaires à la maîtrise des données, et comment allons-nous continuer à développer ces compétences pour nous assurer que tous les élèves quittent nos écoles en tant que jeunes adultes ma&
Aussi disponible : Dans «Ressources: La littératie des données à travers les domaines», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
L’élève utilise le sens du nombre (p. ex., les pourcentages, les taux, les rapports, les conversions) pour modifier un budget en fonction de différentes circonstances.
Cette leçon présente aux élèves les concepts de limites et de l’infini avec un problème pratique de géométrie et de mesure en utilisant le codage et des feuilles de calcul. Les élèves débuteront avec un problème pratique, ensuite, ils enquêteront de façon théorique, comment est-ce que l’aire d’un polygone régulier est influencée lorsque nous augmentons le nombre de côtés tout en gardant le même périmètre. Ils créeront un patron de calcul de l’aire d’un polygone qui tend vers la plus grande aire, un cercle, en ajoutant des accroissements de plus en plus petits. Les patrons seront examinés en utilisant des
En examinant les données qui nous entourent, telles les statistiques sportives et les reportages, les élèves exploreront différentes façons de représenter, d’analyser et de comprendre les données, y compris les valeurs des quartiles et les diagrammes de quartiles.
Cette leçon permet aux élèves de voir comment la croissance des suites visuelles peut être interprétée de différentes manières et comment chacune d’elles se connecte à une représentation algébrique. Ils apprendront alors à montrer que toutes les représentations sont équivalentes.
Cette leçon présente le concept de densité en ce qui concerne les nombres rationnels, tout en explorant les régularités avec des fractions et des puissances dans l'optique d'une règle impériale.
Dans cette leçon, les élèves utiliseront les données canadiennes sur les émissions de CO2 pour déterminer les tendances et faire des prévisions pour l'avenir si nous n'agissons pas et si nous adoptons des statégies de réduction d'émissions.
Cette leçon présente aux élèves certaines des compétences algébriques de base qui seront utilisées dans ce cours et les cours suivants. Les élèves utilisent le CAS (Systèmes d'algèbre par ordinateur ) pour tester une variété d’opérations et d'expressions et rechercher des motifs pour déterminer des propriétés algébriques. Les élèves utilisent également le code pour tester une propriété algébrique, ainsi que pour modifier le code afin d'observer différentes propriétés. Tout au long de la leçon, les élèves identifient et utilisent des ressources et des supports qui les aideront à persévérer dans leur apprentissage des mathématiques et à développer une pensée mathématique critique.
En explorant la fable d'Ésope - Le corbeau et le pichet, les élèves utiliseront l'algèbre et le codage pour résoudre des problèmes de mesure qui permettront le développement de stratégies de résolution de problèmes. Afin de simuler l'histoire dans la fable, les élèves vont recueillir des données et vont développer un modèle algébrique pour ensuite le tester. Les élèves vont consolider des stratégies de résolution de problèmes. Finalement, les élèves vont tester leurs stratégies dans un nouveau défi - le bassin-trempette ("dunk-tank").
Les élèves approfondissent leur compréhension de l'utilisation des ensembles de données nationales à grande échelle en examinant les ensembles de données à un moment précis et sur une période donnée afin de comprendre comment chaque ensemble de données peut être utilisé pour aider à guider les décisions gouvernementales et l'élaboration des politiques. En outre, ils examinent comment les données peuvent potentiellement être mal utilisées. Les élèves examinent également les questions relatives à la collecte et au stockage de données à grande échelle. Les élèves auront l'occasion d'explorer des données sur un sujet de leur choix en fonction de leurs intérêts dans la base de données de Statistique Canada.
Les jeux vidéo sont riches en données. Cette leçon utilise les données disponibles pour Minecraft pour démontrer comment un joueur peut utiliser les données et les mathématiques pour éclairer ses choix afin de prendre de bonnes décisions en jouant aux jeux vidéo.
Dans cette leçon, les élèves vont identifier les relations linéaires et non linéaires dans une variété de contextes. Les élèves vont déterminer les caractéristiques de relations linéaires et non linéaires représentées de diverses façons. Les élèves devront avoir complété la leçon "Comment est-ce que ça grandit?" avant d'entamer celle-ci.
Cette leçon permet aux élèves d'explorer comment la modification d'une ou plusieurs dimensions d'une forme 2D affecte le périmètre/circonférence et/ou l’aire, et comment la modification d'une ou plusieurs dimensions d'un objet 3D affecte l’aire de la surface et/ou le volume. Les élèves utiliseront le codage pour mieux comprendre ces concepts, ce qui leur permettra d'explorer un plus grand nombre d'exemples au courant de la leçon.
Cette leçon permet aux élèves de représenter des relations linéaires à l'aide de matériel concret, de table de valeurs, de graphiques et d'équations, et d'établir des liens entre les diverses représentations pour démontrer une compréhension des taux de variation et des valeurs initiales.
Les élèves vont mesurer le nombre de pas nécessaire pour voyager une distance donnée, comme un tour de piste, et vont l’utiliser pour ensuite faire des analyses et des représentations graphiques de ces données.
Dans cette leçon, les élèves travaillent avec des fractions, des décimales, des pourcentages, des taux et des proportions pour résoudre des problèmes de mesure, de géométrie et de trajectoire. De petites erreurs dans les entrées peuvent avoir des conséquences importantes et inattendues dans les sorties. Autant que l'estimation est souvent utile, dans certaines situations, la précision est d'une importance capitale.
Cette leçon présente aux élèves les relations de la forme x + y = k, 2x + 2y = k et xy = k et utilise ces graphiques comme plateforme pour expliquer l'infini et la densité. Tout au long de la leçon, les élèves créeront des graphiques, à la main ou à l'aide de la technologie, et renforceront leur compréhension de la façon d'utiliser les lignes et/ou les courbes de meilleur ajustement pour découvrir des informations sur la relation.
Dans cette leçon, on utilise la collecte et l’analyse de données afin de tirer des conclusions et faire une prise de conscience sur les bienfaits d’une bonne santé mentale.
Dans cette leçon, les élèves découvriront la relation entre le volume de prismes et de pyramides ainsi que la relation entre le volume de cylindres et de cônes à l’aide de constructions avec des cartons et de discussions en groupe-classe.
Dans cette leçon, les élèves apprendront, avec un partenaire, un concept à l’étude et deviendront les experts de ce concept. Chaque équipe sera invitée par la suite à expliquer leur concept aux autres équipes sous forme de carrousel. À la fin de cette leçon, tous les élèves auront appris six nouveaux concepts : la compréhension du développement des nombres, l’évaluation de puissances, la résolution d’équations, la compréhension du développement et de l’utilisation de relations géométriques, l’analyse de données, et la compréhension des caractéristiques de diverses représentations. Il est suggéré de faire cette leçon en début du cours.
Dans cette leçon, les élèves examinent l’effet de divers facteurs, tels le taux d’intérêt, le coût initial et le montant du versement initial, sur le coût total d’un prêt pour une grande dépense.
Cette leçon explorera les liens entre les rapports, les proportions, les fractions, les pourcentages, les décimaux et la pente en faisant une enquête au sujet de la peinture de l'Homme de Vitruve de Léonard De Vinci. Les élèves utiliseront différents outils, y compris des rubans à mesurer, des feuilles de calcul et une technologie graphique pour recueillir des données, des relations graphiques et développer une compréhension de la régression. Cette leçon s'appuie sur les connaissances préalables des élèves de la 8e année et les incorpore, y compris les diagrammes de dispersion, les relations faibles à fortes entre les variables, les valeurs aberrantes et les droites de meilleur ajustement.
Cette leçon donne aux élèves l'occasion de développer leurs compétences en matière de recherche en travaillant en groupes pour étudier l'histoire des fractions. À la suite de cette leçon structurée, les élèves seront mieux préparés à s'engager dans une recherche individuelle sur un concept mathématique de leur choix.
Cette leçon fournit aux élèves des informations sur un exemple de revenu. Les élèves seront ensuite confrontés à différentes situations pouvant inclure des déductions, des coûts de logement et des coûts liés à la vie quotidienne/mensuelle, le tout utilisé pour modifier un budget. Tout au long de la leçon, les élèves établiront des relations saines et communiqueront efficacement en mathématiques, et développeront une pensée mathématique critique.
Cette leçon expose les élèves aux différentes façons dont l'argent peut fructifier et à certains des risques associés au fait de gagner de grosses sommes d'argent. Cette leçon s'harmonise bien avec le volet Vie saine du programme d'éducation physique de 9e année. Cette leçon peut être utilisée avant les leçons « Partons à l'aventure! » et « Une année future dans la vie d'un élève - Prendre des décisions financières », qui traitent toutes deux de la création de budget.
Les élèves établiront des liens entre les modèles algébriques d'équations linéaires et leurs représentations (graphique/table de valeurs/régularités), et décriront l'effet des représentations lorsqu'une équation est manipulée ou changée de différentes manières.
Les élèves établiront des liens entre les modèles algébriques d'équations linéaires et leurs représentations (graphique/table de valeurs/régularités), et décriront l'effet des représentations lorsqu'une équation est manipulée ou changée de différentes manières.
Ce webinaire présentera aux enseignantes et aux enseignants de l’Ontario trois (3) plans de cours qui présentent trois différentes façons qu’un membre du personnel pourrait structurer le cours de mathématiques de 9e année 2021. Les plans de cours ont été partagés sur notre site web OntarioMath.support. Chaque plan de cours comprend toutes les attentes et les contenus du programme cadre et fournit des suggestions sur comment les regrouper afin de présenter les mathématiques en 9e année comme un tout interrelié. En plus d’une structure de cours, chaque plan présente des idées de questions et de tâches qui permettent d’engager les élèves avec les mathématiques qu’elles et ils apprennent. Dans ce webinaire nous allons aussi présenter les principes sur lesquels les trois plans de cours ont été fondées afin d’appuyer le personnel enseignant dans l’implémentation d’un programme-cadre décloisonné de 9e année.
Aussi disponible : Dans «Ressources: La planification d’un cours», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Comment est-ce qu’une classe décloisonnée est-elle différente? Comment doit-on transformer l’enseignement et l’évaluation afin de respecter ces différences? Dans ce webinaire, nous discutons du but d’assurer le succès de TOUS les élèves, ainsi que des considérations et des idées qui pourront appuyer le personnel enseignant dans leur planification d’un cours de mathématiques.
Aussi disponible : Dans «Ressources: Le décloisonnement pour le succès», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
La création d’un espace d’apprentissage sécuritaire et inclusif, qui encourage la collaboration entre les élèves et les choix des élèves, est incontournable dans la mise en œuvre du programme cadre décloisonné de mathématiques 2021. Dans ce webinaire, nous allons partager des stratégies pratiques qui permettront de surmonter les défis présentés par l’enseignement du nouveau curriculum tout en assurant l’équité et l’inclusion en apportant la voix de l’élève et ses expériences vécues à l’apprentissage des mathématiques.
Aussi disponible : Dans «Ressources: La mise en place de l’environnement d’apprentissage», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Ce webinaire d'une heure se concentrera sur la façon dont le processus de modélisation mathématique, intégré aux concepts mathématiques de 9e année, peut soutenir efficacement le développement de solides compétences en réflexion mathématique chez les élèves. Dans ce webinaire, nous explorerons en détail à quoi ressemble le processus de modélisation mathématique et comment il établit naturellement des liens entre les mathématiques et les autres disciplines, ainsi qu'entre les mathématiques et les cultures et communautés des élèves. Nous espérons que le personnel enseignant comprendra mieux ce qu'est la modélisation mathématique et comment elle peut être intégrée dans un programme de mathématiques. Des exemples de tâches seront aussi discutées.
Aussi disponible : Dans «Ressources: Domaine A - Pensée mathématique et établissement de liens par le modélisation mathématique», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
« En 9e année, les élèves commencent à utiliser le codage comme un outil pour interagir avec les mathématiques. Elles et ils utilisent les habiletés développées au palier élémentaire afin de créer et modifier du code dans multiples environnements de codage, y compris des langages de programmation basé sur du texte, des feuilles de calcul, des modules de calcul formel et des logiciels de création virtuelle graphique et géométrique. » (2021 MTH1W)
Que connaissent les élèves en matière de codage lorsqu'ils arrivent en 9e année? Comment suis-je censé enseigner le codage en même temps que toutes les autres attentes en mathématiques? Comment puis-je soutenir les élèves si je ne sais pas comment coder ? Si vous vous êtes posé certaines de ces questions, venez à ce webinaire pour explorer quelques réponses.
Aussi disponible : Dans «Ressources: Domaine A - Pensée mathématique et établissement de liens par le codage», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
août 2021
Dans ce webinaire sur la transition entre le nouveau programme-cadre révisé de mathématiques de l'élémentaire (2020) et le nouveau programme-cadre révisé de mathématiques de la 9e année (2021), les participants recevront des informations spécifiques sur l'alignement des attentes des 7e, 8e et 9e années. Ils recevront également des conseils sur les approches des plans de cours exemplaires ainsi que sur la planification des leçons et des évaluations. Les références et les ressources disponibles pour soutenir le personnel enseignant seront partagées. Une période de questions et réponses sera incluse dans ce webinaire.
Aussi disponible : Dans "Ressources: La transition d’élémentaire à la 9e année en mathématiques", vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
 Pratiques pédagogiques à fort impact en mathématiques
[PDF]
Pratiques pédagogiques à fort impact en mathématiques
[PDF]
L’utilisation réfléchie de pratiques pédagogiques à fort impact – incluant le fait de savoir quand les utiliser et comment les combiner pour appuyer l’atteinte l'atteinte des attentes et contenus est une composante essentielle dans l’enseignement efficace des mathématiques.
 Planifications - long terme
[URL]
Planifications - long terme
[URL]
Une planification à long terme définit un plan d’un an relatif à l’apprentissage des mathématiques
Ces exemples de planification à long terme présentent les séquences d’enseignement possibles pour l’année scolaire. Il existe de nombreuses façons de structurer une planification d’apprentissage efficace.
 Webinaire 1 - Vision, objectifs et domaines d'étude
[MP4]
Webinaire 1 - Vision, objectifs et domaines d'étude
[MP4]
Ce webinaire d'une heure explorera la vision, les objectifs et les domaines d'étude du nouveau programme-cadre de mathématiques 1re à la 8e de l'Ontario. Ces sections très importantes de la « Mise en contexte » du programme-cadre sont essentielles à considérer dans l'enseignement et l'apprentissage des mathématiques.
Aussi disponible : La présentation du PPT du webinaire 1 - Vision, objectifs et domaines d'étude. [PDF]
 Webinaire 2 - La planification du programme-cadre
[MP4]
Webinaire 2 - La planification du programme-cadre
[MP4]
Ce webinaire d'une heure explorera les différentes considérations concernant la planification du programme-cadre de mathématiques. Un survol des pratiques pédagogiques à fort impact sera également examiné.
Aussi disponible :
* Présentation PPT du webinaire # 2 : « La planification du programme-cadre » [PDF]
* Ressources en lien avec le webinaire # 2 : « La planification du programme-cadre » [Google Doc]
 Webinaire 3 - Modélisation mathématique
[MP4]
Webinaire 3 - Modélisation mathématique
[MP4]
Ce webinaire d'une heure explorera le processus de modélisation mathématique. Le but est d'approfondir la compréhension de ce qu'est le processus de modélisation mathématique chez les pédagogues afin de développer une vision cohérente et commune. Suite au webinaire vous verrez comment ce processus peut être tissé dans votre planification mathématique.
Aussi disponible : Présentation PPT du webinaire # 3 : « modélisation mathématique »
 Webinaire 4 - Apprentissage socioémotionnel en mathématiques
[MP4]
Webinaire 4 - Apprentissage socioémotionnel en mathématiques
[MP4]
Ce webinaire d'une heure explorera le nouveau domaine d'étude : Apprentissage socioemotionnel et les processus mathématiques. Les habiletés socioémotionnelles en lien avec les processus mathématiques seront examinés et vous verrez comment ceux-ci s’intègrent à l’enseignement et l’évaluation des cinq autres domaines mathématiques.
Aussi disponible : Ressources en lien avec le webinaire # 4 : « Apprentissage socioémotionnel en mathématiques » [Google Doc]
 Webinaire 5 - Évaluation et communication du rendement
[MP4]
Webinaire 5 - Évaluation et communication du rendement
[MP4]
Ce webinaire d'une heure explore l'évaluation et la communication du rendement. Nous revisiterons les principes d’évaluation de la politique «Faire croître le succès» à la lumière du programme-cadre révisé de mathématiques.
Aussi disponible : Ressources en lien avec le webinaire # 5 : « Évaluation et communication du rendement » [Google Doc]
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathémat
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle moyen du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathématiques d'un
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle primaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathématiques d'
Une compilation bilingue de vocabulaire pertinent directement lié à la pensée computationnelle et à la programmation/codage.
Un continuum de la 1re à la 8e année décrivant les concepts de codage par niveau, associé à un projet Scratch et des notes pour l'enseignant.e.
Un résumé des matériaux de manipulation virtuel Fractions qui sont disponibles, y compris les liens, et les considérations relatives à leur utilisation.
La présentation PPT du webinaire # 1 : Vision, objectifs et domaines d'étude
Ressources en lien avec le webinaire # 2 : « La planification du programme-cadre »
Présentation PPT du webinaire # 2 : « La planification du programme-cadre »
Présentation PPT du webinaire # 3 : « modélisation mathématique »
Ressources en lien avec le webinaire # 4 : « Apprentissage socioémotionnel en mathématiques » [Google Doc]
Ressources en lien avec le webinaire # 5 : « Évaluation et communication du rendement » [Google Doc]
 Webinaire 1 - Vision, objectifs et domaines d'étude
[MP4]
Webinaire 1 - Vision, objectifs et domaines d'étude
[MP4]
Ce webinaire d'une heure explorera la vision, les objectifs et les domaines d'étude du nouveau programme-cadre de mathématiques 1re à la 8e de l'Ontario. Ces sections très importantes de la « Mise en contexte » du programme-cadre sont essentielles à considérer dans l'enseignement et l'apprentissage des mathématiques.
Aussi disponible : La présentation du PPT du webinaire 1 - Vision, objectifs et domaines d'étude. [PDF]
 Webinaire 2 - La planification du programme-cadre
[MP4]
Webinaire 2 - La planification du programme-cadre
[MP4]
Ce webinaire d'une heure explorera les différentes considérations concernant la planification du programme-cadre de mathématiques. Un survol des pratiques pédagogiques à fort impact sera également examiné.
Aussi disponible :
* Présentation PPT du webinaire # 2 : « La planification du programme-cadre » [PDF]
* Ressources en lien avec le webinaire # 2 : « La planification du programme-cadre » [Google Doc]
 Webinaire 3 - Modélisation mathématique
[MP4]
Webinaire 3 - Modélisation mathématique
[MP4]
Ce webinaire d'une heure explorera le processus de modélisation mathématique. Le but est d'approfondir la compréhension de ce qu'est le processus de modélisation mathématique chez les pédagogues afin de développer une vision cohérente et commune. Suite au webinaire vous verrez comment ce processus peut être tissé dans votre planification mathématique.
Aussi disponible : Présentation PPT du webinaire # 3 : « modélisation mathématique »
 Webinaire 4 - Apprentissage socioémotionnel en mathématiques
[MP4]
Webinaire 4 - Apprentissage socioémotionnel en mathématiques
[MP4]
Ce webinaire d'une heure explorera le nouveau domaine d'étude : Apprentissage socioemotionnel et les processus mathématiques. Les habiletés socioémotionnelles en lien avec les processus mathématiques seront examinés et vous verrez comment ceux-ci s’intègrent à l’enseignement et l’évaluation des cinq autres domaines mathématiques.
Aussi disponible : Ressources en lien avec le webinaire # 4 : « Apprentissage socioémotionnel en mathématiques » [Google Doc]
 Webinaire 5 - Évaluation et communication du rendement
[MP4]
Webinaire 5 - Évaluation et communication du rendement
[MP4]
Ce webinaire d'une heure explore l'évaluation et la communication du rendement. Nous revisiterons les principes d’évaluation de la politique «Faire croître le succès» à la lumière du programme-cadre révisé de mathématiques.
Aussi disponible : Ressources en lien avec le webinaire # 5 : « Évaluation et communication du rendement » [Google Doc]
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente de codage du domaine d’algèbre pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Nous ferons un survol des leçons qui ont été créées pour appuyer les enseignantes et les enseignants de l'Ontario ainsi que la pédagogie et les habiletés socioémotionnelles que le codage apporte à votre classe.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
Bienvenue à ce webinaire sur le codage en lien avec notre nouveau programme-cadre de Mathématiques 2020. Nous vous ferons découvrir la pédagogie et les habiletés socioémotionnelles que le codage apporte dans votre classe, ainsi que les leçons qui ont été créées pour aider les enseignants de l'Ontario au cycle moyen.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
Bienvenue à ce webinaire sur le codage en lien avec notre nouveau programme-cadre de Mathématiques 2020. Nous vous ferons découvrir la pédagogie et les habiletés socioémotionnelles que le codage apporte dans votre classe, ainsi que les leçons qui ont été créées pour aider les enseignant.e.s de l'Ontario au cycle primaire.
NOTE : Cet enregistrement ne contient pas encore la section des questions et réponses - celle-ci sera bientôt ajoutée à partir de tous les enregistrements avec sous-titrage.
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle primaire du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle primaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. L'objectif des leçons était de fournir des contextes réels pour que les élèves développent leur compréhension
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle primaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathématiques d'
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle moyen du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle moyen du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. Les scénarios donnent l'occasion d'avoir une discussion sur les choix financiers et les inégalités d'accès à ces cho
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle moyen du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathématiques d'un
Bienvenue à ce webinaire sur l'enseignement du domaine de Nombres pour le cycle intermédiaire du programme révisé de mathématiques.Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons sur le domaine de Nombres sont axées sur le développement des concepts et des habiletés liés aux fractions. Ces leçons mettent en valeur les dernières recherches sur l'apprentissage des fractions, notamment l'accent mis sur la représentation visuelle.
Bienvenue à ce webinaire sur l'enseignement du nouveau domaine de littératie financière pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous vous présentons les leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Lors de l'élaboration des leçons de littératie financière pour ce projet, il a été décidé d'utiliser des tâches basées sur des scénarios. Les scénarios donnent l'occasion d'avoir une discussion sur les choix financiers et les inégalités d'accès &
Bienvenue à ce webinaire sur l'enseignement de la nouvelle attente du processus de modélisation mathématique du domaine d'algèbre pour le cycle intermédiaire du programme-cadre révisé de mathématiques. Dans ce webinaire, nous ferons un survol des leçons qui ont été créées par des éducateurs de l'Ontario pour appuyer les éducateurs de l'Ontario. Ces leçons de modélisation mathématique visent à développer l'appréciation des élèves pour le rôle que jouent les mathématiques dans la « vraie » vie, tout en leur donnant l'occasion de vivre l'expérience des mathémat
août 2021
Dans ce webinaire sur la transition entre le nouveau programme-cadre révisé de mathématiques de l'élémentaire (2020) et le nouveau programme-cadre révisé de mathématiques de la 9e année (2021), les participants recevront des informations spécifiques sur l'alignement des attentes des 7e, 8e et 9e années. Ils recevront également des conseils sur les approches des plans de cours exemplaires ainsi que sur la planification des leçons et des évaluations. Les références et les ressources disponibles pour soutenir le personnel enseignant seront partagées. Une période de questions et réponses sera incluse dans ce webinaire.
Aussi disponible : Dans "Ressources: La transition d’élémentaire à la 9e année en mathématiques", vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Ce webinaire présentera aux enseignantes et aux enseignants de l’Ontario trois (3) plans de cours qui présentent trois différentes façons qu’un membre du personnel pourrait structurer le cours de mathématiques de 9e année 2021. Les plans de cours ont été partagés sur notre site web OntarioMath.support. Chaque plan de cours comprend toutes les attentes et les contenus du programme cadre et fournit des suggestions sur comment les regrouper afin de présenter les mathématiques en 9e année comme un tout interrelié. En plus d’une structure de cours, chaque plan présente des idées de questions et de tâches qui permettent d’engager les élèves avec les mathématiques qu’elles et ils apprennent. Dans ce webinaire nous allons aussi présenter les principes sur lesquels les trois plans de cours ont été fondées afin d’appuyer le personnel enseignant dans l’implémentation d’un programme-cadre décloisonné de 9e année.
Aussi disponible : Dans «Ressources: La planification d’un cours», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Comment est-ce qu’une classe décloisonnée est-elle différente? Comment doit-on transformer l’enseignement et l’évaluation afin de respecter ces différences? Dans ce webinaire, nous discutons du but d’assurer le succès de TOUS les élèves, ainsi que des considérations et des idées qui pourront appuyer le personnel enseignant dans leur planification d’un cours de mathématiques.
Aussi disponible : Dans «Ressources: Le décloisonnement pour le succès», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
La création d’un espace d’apprentissage sécuritaire et inclusif, qui encourage la collaboration entre les élèves et les choix des élèves, est incontournable dans la mise en œuvre du programme cadre décloisonné de mathématiques 2021. Dans ce webinaire, nous allons partager des stratégies pratiques qui permettront de surmonter les défis présentés par l’enseignement du nouveau curriculum tout en assurant l’équité et l’inclusion en apportant la voix de l’élève et ses expériences vécues à l’apprentissage des mathématiques.
Aussi disponible : Dans «Ressources: La mise en place de l’environnement d’apprentissage», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
« En 9e année, les élèves commencent à utiliser le codage comme un outil pour interagir avec les mathématiques. Elles et ils utilisent les habiletés développées au palier élémentaire afin de créer et modifier du code dans multiples environnements de codage, y compris des langages de programmation basé sur du texte, des feuilles de calcul, des modules de calcul formel et des logiciels de création virtuelle graphique et géométrique. » (2021 MTH1W)
Que connaissent les élèves en matière de codage lorsqu'ils arrivent en 9e année? Comment suis-je censé enseigner le codage en même temps que toutes les autres attentes en mathématiques? Comment puis-je soutenir les élèves si je ne sais pas comment coder ? Si vous vous êtes posé certaines de ces questions, venez à ce webinaire pour explorer quelques réponses.
Aussi disponible : Dans «Ressources: Domaine A - Pensée mathématique et établissement de liens par le codage», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Ce webinaire d'une heure se concentrera sur la façon dont le processus de modélisation mathématique, intégré aux concepts mathématiques de 9e année, peut soutenir efficacement le développement de solides compétences en réflexion mathématique chez les élèves. Dans ce webinaire, nous explorerons en détail à quoi ressemble le processus de modélisation mathématique et comment il établit naturellement des liens entre les mathématiques et les autres disciplines, ainsi qu'entre les mathématiques et les cultures et communautés des élèves. Nous espérons que le personnel enseignant comprendra mieux ce qu'est la modélisation mathématique et comment elle peut être intégrée dans un programme de mathématiques. Des exemples de tâches seront aussi discutées.
Aussi disponible : Dans «Ressources: Domaine A - Pensée mathématique et établissement de liens par le modélisation mathématique», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.
Les élèves de l'Ontario vivent dans un monde complexe qui est régi par les données. Ce monde évolue et l'émergence de nouveaux domaines et de nouvelles carrières nécessite des personnes ayant un niveau élevé de littératie des données. Soutenir les élèves dans l'acquisition de compétences critiques en littératie des données est une composante essentielle du nouveau curriculum de 9e année décloisonné. La littératie des données est différente de la gestion des données. Bien sûr, les compétences en gestion des données sont aussi importantes pour analyser les données. Dans le cadre du programme-cadre de mathématiques élémentaire révisé en 2020, les élèves ont développé leurs compétences en gestion des données. Comment les relier à l'objectif plus large de la littératie des données ? Quelles sont les compétences nécessaires à la maîtrise des données, et comment allons-nous continuer à développer ces compétences pour nous assurer que tous les élèves quittent nos écoles en tant que jeunes adultes ma&
Aussi disponible : Dans «Ressources: La littératie des données à travers les domaines», vous trouverez des liens vers des recherches, des vidéos, des fichiers audio et des sites Web qui pourraient vous être utiles pour continuer à en apprendre davantage sur le programme révisé de mathématiques (2021).
Ce document est un Google Doc, en mode affichage seulement. Si vous le souhaitez, vous pouvez utiliser Fichier -> Télécharger, ou Fichier -> Faire une copie, pour enregistrer une version pour vous-même.













































